级数不等式的证明题是一种常见的问题，利用导数证明级数不等式更是一种典型问题，有好多学生，甚至老师对这类问题很畏惧，其实只要抓住这类问题的本质进行合理的处理，问题就可以迎刃而解了．要解决这类问题，通常需要分析通项，得到一个不等关系，然后累加即可得到要证明的式子．例如：要证明

，只要证明，再注意一下时的式子即可．

例 已知函数，

，．

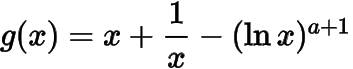
（1）若在定义域内恒成立，求的取值范围；

（2）当取（1）中的最大值时，求函数的最小值；

（3）证明不等式

．

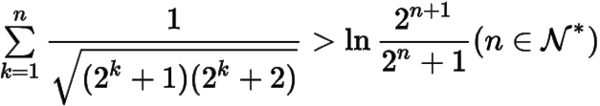
——提问者：888888中山大学 2016-09-19 00:23

分析本题的第一、第二问都是基础题，考查利用导数研究函数的最值问题，难点显然在第三问．事实上，前两问都是为第三问做准备的，下面来看一下具体的解析过程．

解（解答者：df0817）

（1）由题意有在恒成立，令则

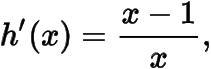
在单调递减，在单调递增，所以于是．

（2）由题意

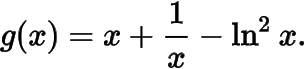
求导

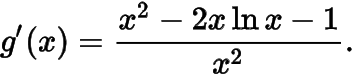
令则所以在上单调递增，注意到所以在单调递减，在单调递增，所以即的最小值为．

（3）级数不等式的通项为

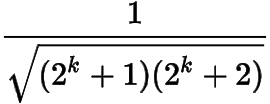
，分析通项

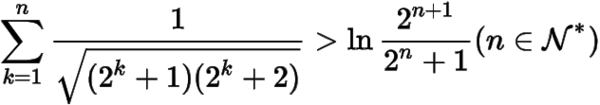
只需证明

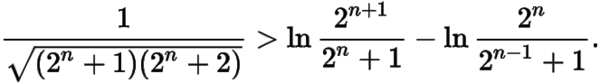
即

这个式子的证明可以借助第二问中的结论，由（2）可得

即

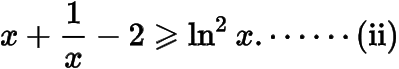
分析(i)(ii)两式可设

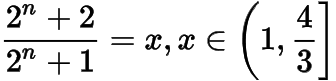
则

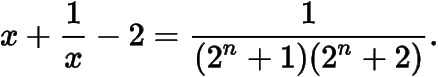
于是(i)式成立，所以得证．

注解决本题时，分析通项是关键．在解题时，可以把已知的函数不等式和要证的通项进行对照，必要时可以通过合理的变形，把它们联系起来．

练习

1．已知函数．

（1）若函数在其定义域上为增函数，求的取值范围；

（2）设

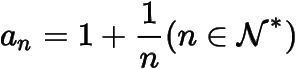
，求证：

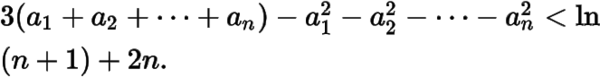
——提问者：weilew 2016-09-19 09:42

2．已知函数

，且在

处的切线方程为．

（1）求 的解析式；

（2）证明：当时，恒有；

（3）证明：若，且

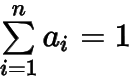
，则

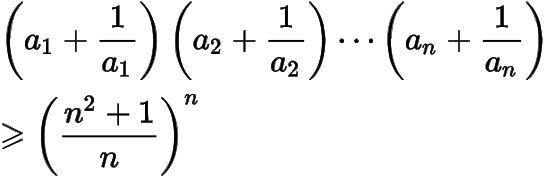
——提问者：Imagine 2016-09-04 11:30

3．求证：当且时，

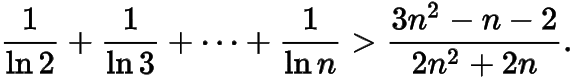
——提问者：湫兮如风凄兮如雨 2016-09-15 09:04

答案

1．（1）；（2）略

2．（1）

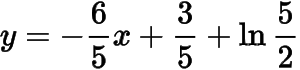
；（2）（3）略

3．略

备注：若要查阅详细的解答过程，请在光子问答APP中搜索用户名，查看用户提问的问题，找到对应时间所发的题即可．