比较几个数(幂或对数)的大小是指数函数、对数函数和幂函数性质的重要应用,常用的方法有单调性法和搭桥法,有时也可利用图象、作差与作商等进行辅助分析.在具体解题过程中,应先观察要比较的数的特征再选用合适的方法比较大小,有时需要先结合幂与对数的运算性质对要比较的数进行合理的变形,再进行大小比较.
例(1)已知,
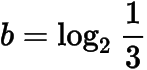
,

,则
A.
B.
C.
D.
——提问者:熊攀 2016-09-17 09:40
(2)设,,,则
A.
B.
C.
D.
——提问者:阿鹏\ 2016-09-18\ 13:43
解(1)(解答者:上善若水任方圆)
因为在 上为增函数,值域为,所以即又因为在上为增函数,所以
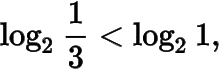
即因为在上为减函数,所以

即 因此故答案为D.
(2)(解答者:燕子)
由对数运算法则有
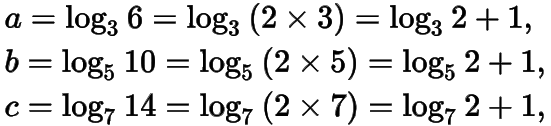
在同一坐标系中,的图象如下:
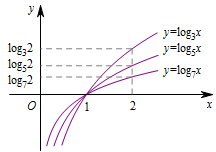
因此所以故答案为D.
注在幂或对数的大小比较中:
(1)若底数相同,但指数(或真数)不同时,可利用指数(或对数)函数的单调性比较大小.例如,要比较和,和的大小可以分别利用指数函数和对数函数的单调性比较.
(2)若底数不同,但指数相同时,可利用幂函数的单调性比较大小.例如,比较和的大小,可以利用幂函数的单调性比较.
(3)若底数不同,指数也不同以及一些对数值共同比大小的可以利用搭桥法(常用和比较.例如,要比较,和的大小可以利用和搭桥比较.
(4)作差、作商与图象法也是常用的技巧.例如:设,,比较和的大小用作差法比较简单些, 而比较,和的大小用图象法简单些.
拓展有些指对幂的值比较大小时,还可能要构造合适的函数,利用导数证明出相应的单调性进行大小比较.感兴趣的读者可尝试运用此方法比较与的大小.
练习
1.设 ,,
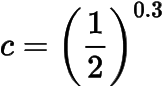
,则 ,, 大小关系为______.
——提问者:风行者 2016-10-17 11:14
2.若 ,,则
A.
B.
C.
D.
——提问者:风行者 2016-10-17 11:17
3.当

时,,则 的取值范围是______.
——提问者:阿鹏 2016-08-29 10:39
答案
1.;
2.B;
3.

.
备注:若要查阅详细的解答过程,请在光子问答APP中搜索用户名,查看用户提问的问题,找到对应时间所发的题即可.
