混搭的英文单词为Mix and Match,即混合搭配,就是将传统上由于地理条件、文化背景、风格、质地等的不同而不同的元素进行搭配,组成有个性特征的新组合体,从而混合搭配出完全个人化的风格.

由于高考试题的题量的限制,高考命题也流行“混搭”风
作为历年高考命题的重点与热点,函数图像的识别与应用问题,也呈现出“混搭”的风格.

1、“搭建型”混搭
函数图像的识别问题多以基本初等函数的图像为基础进行各种变形,多涉及两类不同的基本初等函数,如指数函数、对数函数、幂函数以及三角函数等.
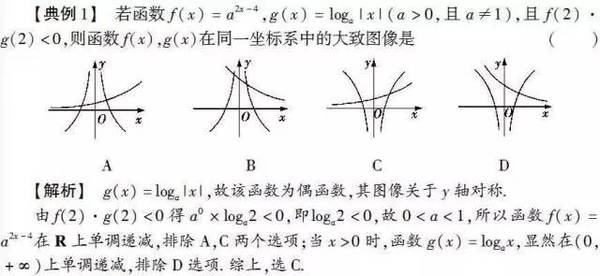
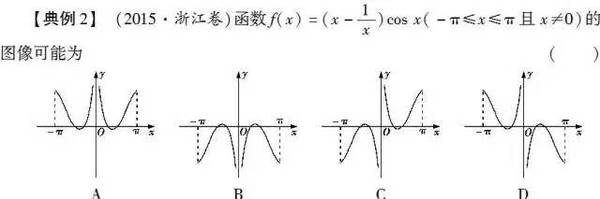
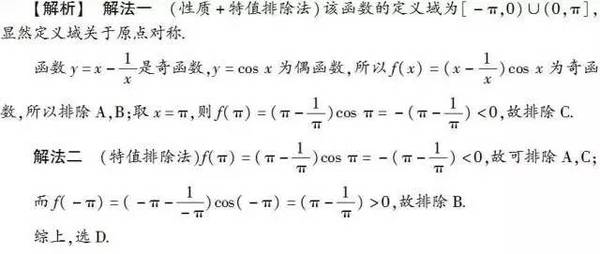
【名师支招】函数图像的识别问题多以基本初等函数的图像为基础进行各种变形,多涉及两类不同的基本初等函数,如指数函数、对数函数、幂函数以及三角函数等.
2、“复合型”混搭
函数图像问题中涉及的复合函数多由指数函数、对数函数、幂函数、一次函数、二次函数以及三角函数等构成.
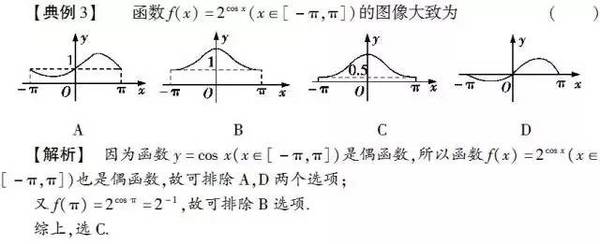
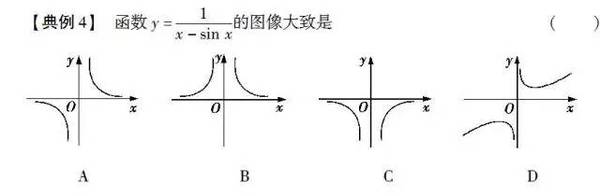

【名师支招】解决函数图像的“复合型”混搭问题,关键是熟练把握复合函数的性质判断方法,特别是函数奇偶性与单调性的综合判断方法,可借助导数进行一些初步的分析,进而结合选项的不同及其与函数解析式的对应,利用排除法解决.
3、“跨界型”混搭
函数图像的识别问题除了与基本初等函数之间的“搭建型”与“复合型”混搭之外,还可以与解三角形、圆锥曲线、立体几何等模块知识进行“跨界”混搭,涉及的知识面更宽.



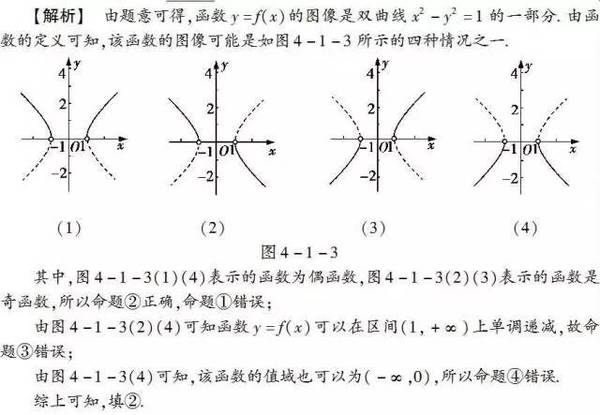
【名师支招】解决函数图像的“跨界型”混搭问题,不仅要熟练掌握基本初等函数的图像和性质,还要注意其他知识模块对应知识的灵活运用与转化,确定问题的实质,根据所涉及模块知识的特点,利用相关图形的直观性、对称性等进行解题.
总之,对于函数图像的识别问题,要抓住选项与函数解析式的特点,找到切入点,灵活利用排除法进行解决.
