曲线是平面内到定点的距离与到定直线的距离的距离之和为的动点的轨迹,则曲线与轴的交点的横坐标是_____;又已知(为参数),那么的最小值______.
答案,
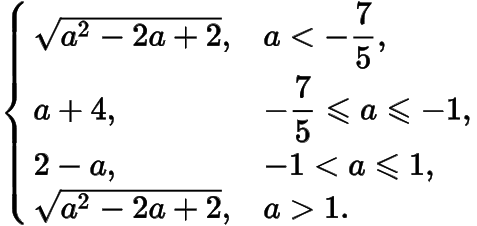
.
分析与解作与直线的距离为的两条直线,,那么“到定点与定直线的距离之和为”,就转化成了“在直线的左侧到定点的距离与到直线的距离相等,或在直线的右侧到定点的距离与到直线的距离相等”,如图.
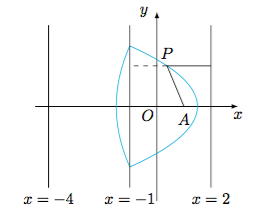
曲线由抛物线弧
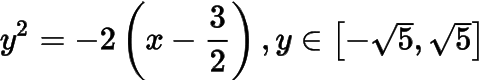
和抛物线弧
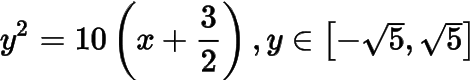
共同组成.
容易求出曲线与轴的交点坐标为.
接下来研究对于,的最小值.
如下图,设直线与直线,抛物线弧
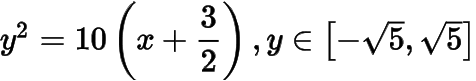
,直线,抛物线弧
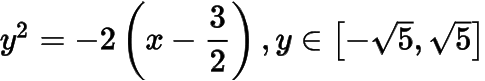
,直线依次交于,
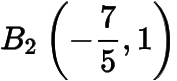
,,,.
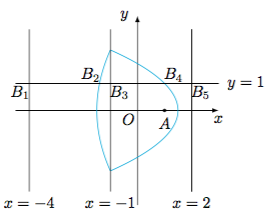
以为分界点分类讨论:
当点位于的左侧或的右侧(即“钟形”外部)时,的最小值为,当点为线段与曲线的交点时取到最小值;
当点位于之间时,若点在左侧抛物线弧上,则有其中表示点到的距离;若点在右侧抛物线弧上,则有其中表示点到的距离,等号都能取到.再比较与的大小即可得
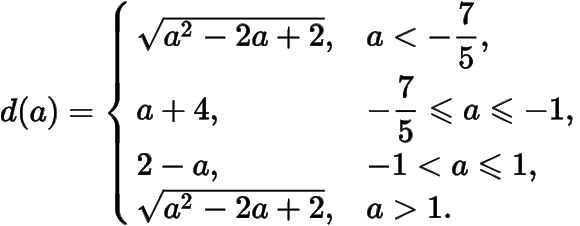
思考与总结本题是抛物线描述:“到定点与定直线距离之差为定值”的升级版本,需要补充辅助线.解决问题的关键是利用抛物线的定义将到定点的距离转化为到定直线的距离.
