08：00-24:00
已知函数与函数
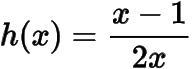
()的图象有且只有一条公切线，求实数的值．
分析与解 法一 分离
由于函数的导函数分别为
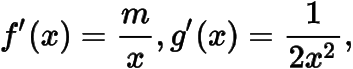
设公切线与函数与函数的图象分别相切于与
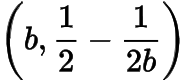
，则
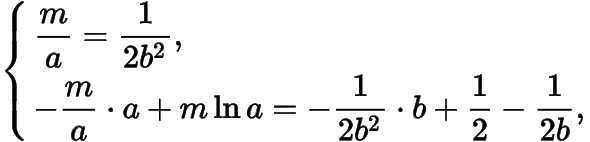
从而
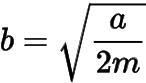
，且
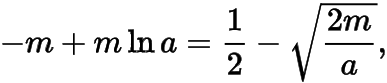
即
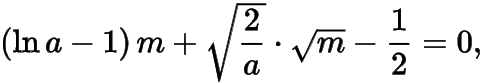
于是
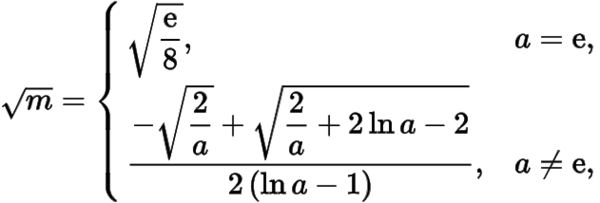
即
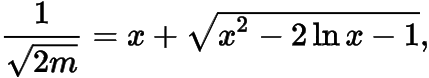
其中
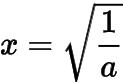
．记上述等式右边为，对求导得
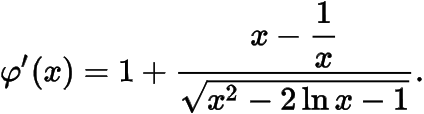
可以证明当时，；当时，（可以利用与
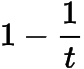
的大小关系得到与
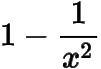
的大小关系，从而得到结论）．
从而有在上单调递减，在上单调递增．当时，取得最小值．因此当
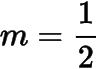
时，符合题意．
综上所述，实数的值为，对应的公切线方程为
．
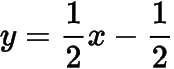
法二 不分离
在点处的切线为
而在点
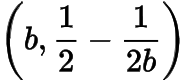
处的切线为
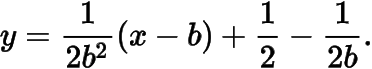
由这两条切线重合知
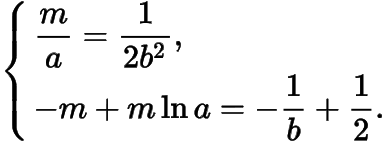
问题即当在什么范围内时，关于的方程有唯一一组解．因为与的值一一对应，如果在方程组中消去，得到
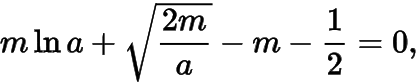
此方程组对有唯一解，不好计算；
如果在方程组中消去得到
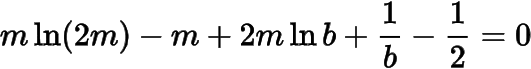
对有唯一解，记左边为，则有
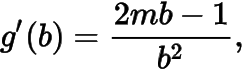
方程组有解时有，所以在
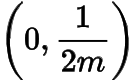
上单调递减，在
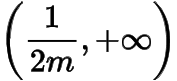
上单调递增，所以
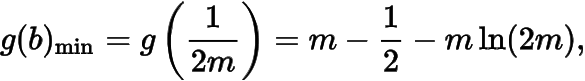
而当与时，均有，所以当且仅当这个最小值等于零时方程有唯一解．
最后解方程
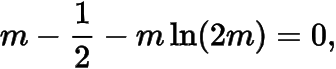
显然
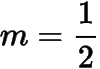
是它的解，考虑
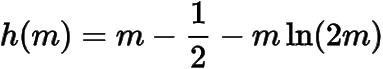
，有，所以在
上单调递增，在
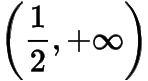
上单调递减，所以是的唯一解，所以
根据学生的高考分数、意向专业 为您查找适合你的院校列表， 24小时内短信电话发送给你！
