极化恒等式设是两个平面向量,则成立恒等式

有时也将上式写成
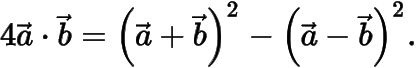
例已知是圆上的两个点,是线段上的动点,当的面积最大时,则
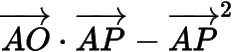
的最大值是______.
——提问者:风行者 2016-08-03 11:01
分析注意到
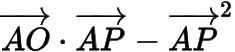
可变形为,因此,可尝试利用极化恒等式进行思考.
解(答题者:意琦行)
设,结合,则

因此,当,即时,面积最大.所以
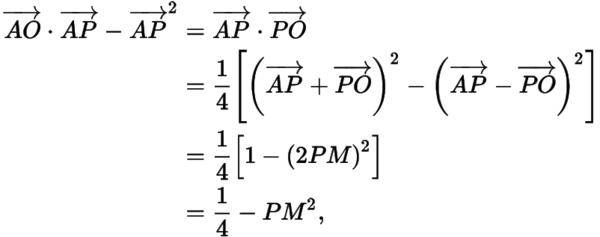
其中为的中点,如图:
此时的最小值为
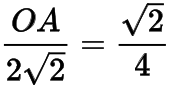
,故所求最大值为
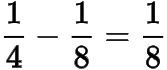
.
总结极化恒等式的主要作用在于,它可以将两向量的数量积转化为这两个向量的“和向量”与“差向量”,因此,当两个向量的“和向量”或“差向量”为定向量时,常常可以考虑利用极化恒等式进行转化求解.
练习
1.如图放置的正方形,,分别在轴、轴的正半轴(含原点)上滑动,则的最大值为______.
——提问者:风行者 2016-09-09 10:10
2.在等腰直角三角形 中,,点 为斜边 的中点,点 在线段 上运动,则
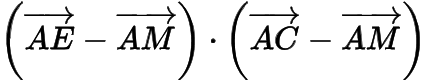
的取值范围是( )
A.
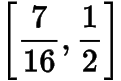
B.
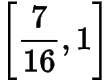
C.
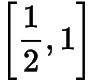
D.
——提问者:了然无声 2016-10-13 11:53
3.如图,在中,是的中点,是上的两个三等分点,,,则的值是______.
——提问者:weilew 2016-08-24 11:43
答案
1.;
2.A;
3..
备注:若要查阅详细的解答过程,请在光子问答APP中搜索用户名,查看用户提问的问题,找到对应时间所发的题即可.
