08：00-24:00
已知椭圆
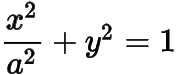
的离心率为
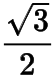
，为圆上任意一点，过作椭圆的两条切线．设切点分别为．
(1) 证明：切线的方程为
；
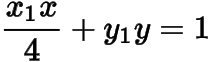
(2) 设为坐标原点，求面积的最大值．
分析与解(1) 椭圆的方程为
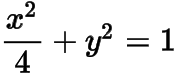
．设点的方程为
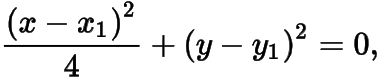
利用交点曲线系可得切线的方程为
整理得
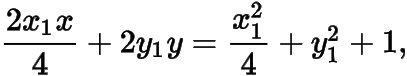
由于
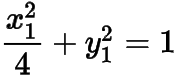
，可得
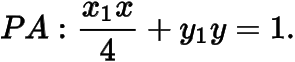
(2) 作仿射变换，，则问题等价于从椭圆
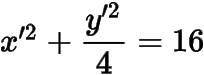
上点引圆的两条切线，切点分别为，求的面积的最大值的一半．的面积只与有关，设()，则
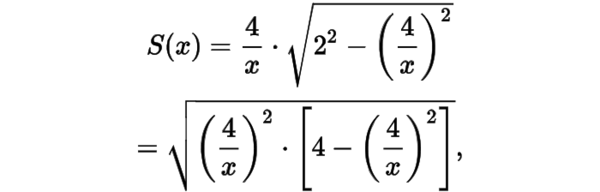
由于
的取值范围是
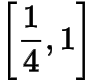
，于是的取值范围是
，其最大值为．回到原问题，所求的面积的最大值为
．
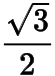
注由曲线系得到的方程是过点的直线，且椭圆上不存在另外一个点也在此直线上，所以它是切线的方程．
根据学生的高考分数、意向专业 为您查找适合你的院校列表， 24小时内短信电话发送给你！
