答案.
分析与解注意到是函数的零点,而不是函数的零点,于是问题等价于函数
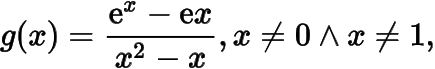
的图象与直线
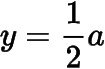
有两个公共点.函数的导函数
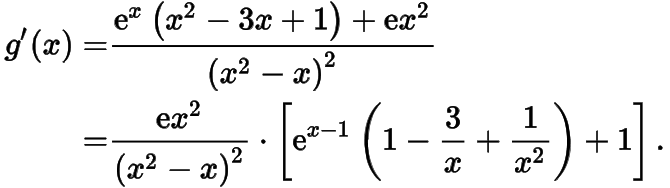
设函数
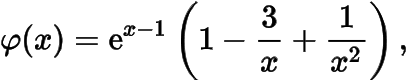
则其导函数

于是的最小值为.这样我们就得到了在,,上均单调递增.显然在上,;在上;在上.于是当时,函数的图象与直线
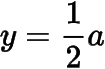
至多只有一个公共点,不符合题意.
接下我们证明当时,函数的图象与直线
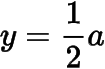
恰好有两个公共点,它们的横坐标分别位于区间和.证明的关键在于在每个区间上,对于任意给定的正数,都存在比大的函数值以及比小的函数值.
在区间上,由于
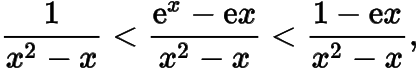
而在区间上,函数

可以取到比大的函数值,而函数
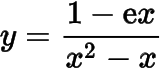
可以取到比小的函数值;
在区间上,一方面由积分两次可得
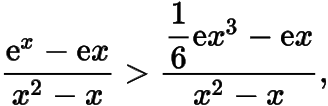
而在区间上,函数
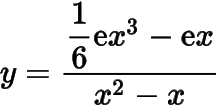
可以取到比大的函数值;另一方面,在区间上,有

而在区间上,函数
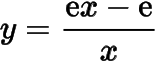
可以取到比小的函数值.
综上,实数的取值范围是.
注对在上进行积分得

再积分一次即可得到
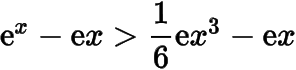
,也可以直接证明此不等式,但积分可以得到这个不等式的样子,我们希望分子是一个三次函数.
另法对求导得从而有当时,,单调递增,从而最多有两个单调区间,不可能有三个不同的零点;
当时,先减后增,最小值为,而,所以一定有两个零点,记为,且有.
而当时,可以取到正数;时,可以取到正数(严格来说,需要对进行放缩以证明或者取出特殊点,同原题方法).所以在上单调递增,在上单调递减,在上单调递增,而,所以,而在时可以取到负值,在时可以取到正数(仍然需要严格处理函数,同原题方法),所以此时一定有三个零点,所以的取值范围是.
