08：00-24:00
2012年新课标 I 卷理科数学第21题：
已知函数满足
．
(1) 求的解析式及单调区间；
(2) 若
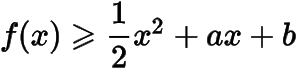
，求的最大值．
分析与解(1) 根据题意，函数的导函数分别令和，可得
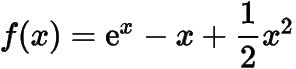
．进而其导函数于是函数的单调递增区间是，单调递减区间是．
(2) 根据题意，有取函数的斜率为的切线，设切点为，则切线方程为其中．易知等号当且仅当时取得．因此．由于，于是记右侧函数为，则其导函数于是当
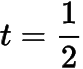
时，取得极大值，亦为最大值．于是的最大值为，此时，
．
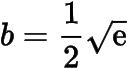
思考与总结从图形的角度看待题中的不等式，将含有两个变元的式子转化为只含一个变元的式子．
下面给出一道练习：
练习已知，且．若在的定义域内恒有，求的最大值．
答案
．
提示时不等式显然不会恒成立，只考虑，此时有
等号当且仅当
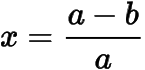
时取到，从而得到，有右边的式子的最大值为
根据学生的高考分数、意向专业 为您查找适合你的院校列表， 24小时内短信电话发送给你！
